二叉搜索树（Binary Search Tree）

在计算机科学中，二叉搜索树（Binary Search Tree，BST），有时也被称为有序或排序二叉树，是一种特殊的容器数据结构，用于在内存中存储“项”（例如数字、名称等）。它们允许快速查找、添加和删除项，并可用于实现动态集合或查找表，通过键（例如通过名称查找人的电话号码）来查找项。

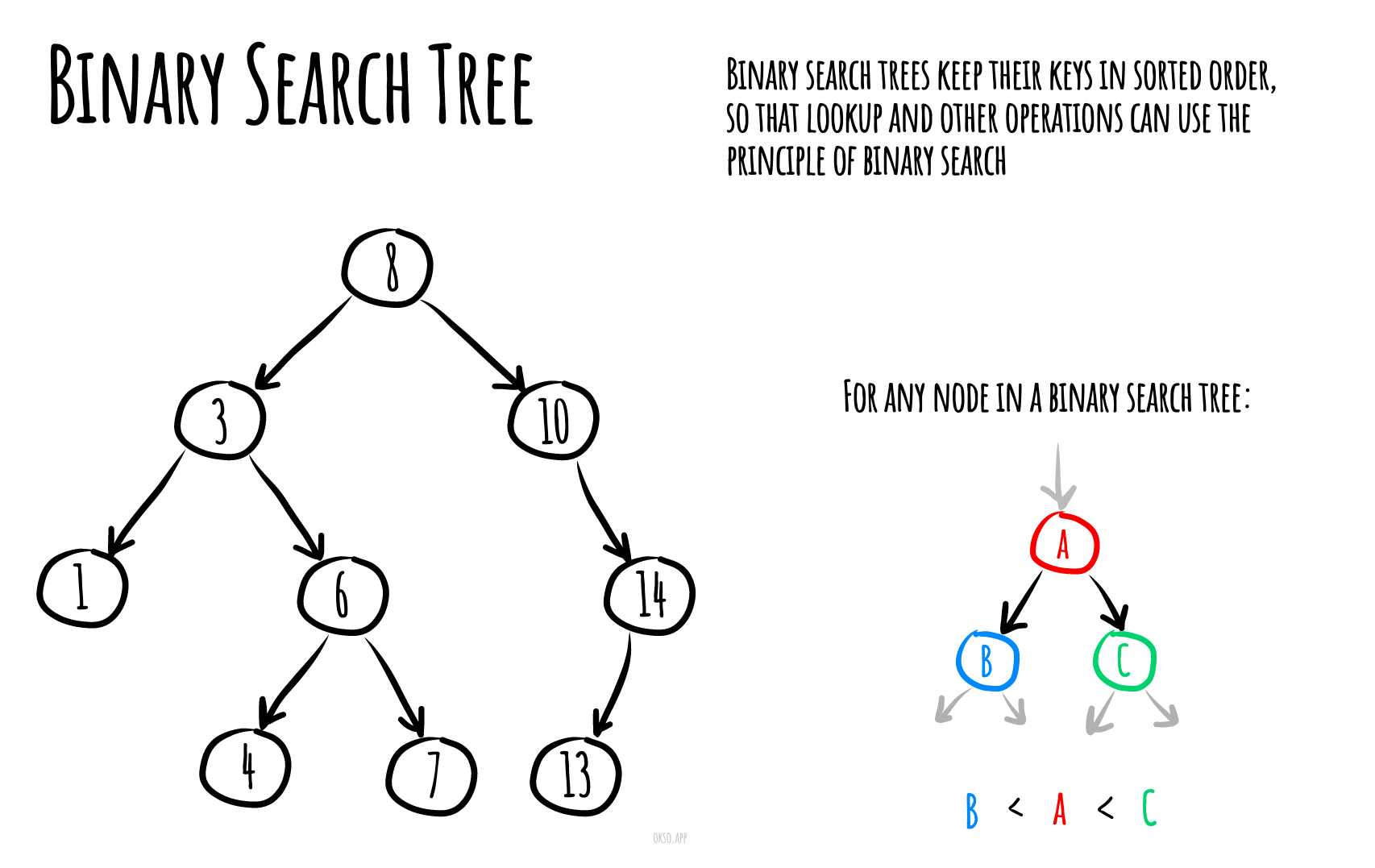
二叉搜索树保持其键的有序性，以便查找和其他操作可以利用二分查找的原理：在树中从根到叶子进行遍历，通过与树节点中存储的键进行比较，并根据比较结果决定是继续在左子树还是右子树中查找。平均而言，这意味着每次比较可以跳过树的大约一半的节点，因此每次查找、插入或删除的时间与存储在树中的项的数量的对数成比例。这比在（未排序的）数组中按键查找项所需的线性时间要好得多，但比哈希表的相应操作要慢。

一个大小为9、深度为3的二叉搜索树，根节点为8。 未绘制叶子节点。

二叉搜索树

基本操作的伪代码

插入

insert(value)
  前置条件：value已通过自定义类型检查，类型为T
  后置条件：value已放置在树的正确位置
  如果 root = ø
    root ← 节点(value)
  否则
    insertNode(root, value)
  结束如果
结束插入

insertNode(current, value)
  前置条件：current为起始节点
  后置条件：value已放置在树的正确位置
  如果 value < current.value
    如果 current.left = ø
      current.left ← 节点(value)
    否则
      InsertNode(current.left, value)
    结束如果
  否则
    如果 current.right = ø
      current.right ← 节点(value)
    否则
      InsertNode(current.right, value)
    结束如果
  结束如果
结束insertNode

查找

contains(root, value)
  前置条件：root为树的根节点，value为要查找的值
  后置条件：确定value是否被找到
  如果 root = ø
    返回 false
  结束如果
  如果 root.value = value
    返回 true
  否则，如果 value < root.value
    返回 contains(root.left, value)
  否则
    返回 contains(root.right, value)
  结束如果
结束contains

删除

remove(value)
  前置条件：value为要删除的节点的值，root为BST的根节点，count为BST中的项数
  后置条件：如果找到并删除了值为value的节点，则返回true；否则返回false
  nodeToRemove ← findNode(value)
  如果 nodeToRemove = ø
    返回 false
  结束如果
  parent ← findParent(value)
  如果 count = 1
    root ← ø
  否则，如果 nodeToRemove.left = ø 并且 nodeToRemove.right = ø
    如果 nodeToRemove.value < parent.value
      parent.left ←  nodeToRemove.right
    否则
      parent.right ← nodeToRemove.right
    结束如果
  否则，如果 nodeToRemove.left != ø 并且 nodeToRemove.right != ø
    next ← nodeToRemove.right
    当 next.left != ø
      next ← next.left
    结束循环
    如果 next != nodeToRemove.right
      remove(next.value)
      nodeToRemove.value ← next.value
    否则
      nodeToRemove.value ← next.value
      nodeToRemove.right ← nodeToRemove.right.right
    结束如果
  否则
    如果 nodeToRemove.left = ø
      next ← nodeToRemove.right
    否则
      next ← nodeToRemove.left
    结束如果
    如果 root = nodeToRemove
      root = next
    否则，如果 parent.left = nodeToRemove
      parent.left = next
    否则，如果 parent.right = nodeToRemove
      parent.right = next
    结束如果
  结束如果
  count ← count - 1
  返回 true
结束remove

查找节点的父节点

findParent(value, root)
  前置条件：value为要查找其父节点的节点的值，root为BST的根节点

且不为ø
  后置条件：如果找到value的父节点，则返回对其的引用；否则返回ø
  如果 value = root.value
    返回 ø
  结束如果
  如果 value < root.value
    如果 root.left = ø
      返回 ø
    否则，如果 root.left.value = value
      返回 root
    否则
      返回 findParent(value, root.left)
    结束如果
  否则
    如果 root.right = ø
      返回 ø
    否则，如果 root.right.value = value
      返回 root
    否则
      返回 findParent(value, root.right)
    结束如果
  结束如果
结束findParent

查找节点

findNode(root, value)
  前置条件：value为要查找的节点的值，root为BST的根节点
  后置条件：如果找到了值为value的节点，则返回对该节点的引用；否则返回ø
  如果 root = ø
    返回 ø
  结束如果
  如果 root.value = value
    返回 root
  否则，如果 value < root.value
    返回 findNode(root.left, value)
  否则
    返回 findNode(root.right, value)
  结束如果
结束findNode

查找最小值

findMin(root)
  前置条件：root为BST的根节点
  后置条件：定位到BST中的最小值
  如果 root.left = ø
    返回 root.value
  结束如果
  findMin(root.left)
结束findMin

查找最大值

findMax(root)
  前置条件：root为BST的根节点
  后置条件：定位到BST中的最大值
  如果 root.right = ø
    返回 root.value
  结束如果
  findMax(root.right)
结束findMax

遍历

中序遍历

inorder(root)
  前置条件：root为BST的根节点
  后置条件：以中序遍历的顺序访问BST中的节点
  如果 root != ø
    inorder(root.left)
    输出 root.value
    inorder(root.right)
  结束如果
结束inorder

前序遍历

preorder(root)
  前置条件：root为BST的根节点
  后置条件：以前序遍历的顺序访问BST中的节点
  如果 root != ø
    输出 root.value
    preorder(root.left)
    preorder(root.right)
  结束如果
结束preorder

后序遍历

postorder(root)
  前置条件：root为BST的根节点
  后置条件：以后序遍历的顺序访问BST中的节点
  如果 root != ø
    postorder(root.left)
    postorder(root.right)
    输出 root.value
  结束如果
结束postorder

完整代码

BinarySearchTreeNode

import BinaryTreeNode from '../BinaryTreeNode';
import Comparator from '../../../utils/comparator/Comparator';

export default class BinarySearchTreeNode extends BinaryTreeNode {
  /**
   * @param {*} [value] - node value.
   * @param {function} [compareFunction] - comparator function for node values.
   */
  constructor(value = null, compareFunction = undefined) {
    super(value);

    // This comparator is used to compare node values with each other.
    this.compareFunction = compareFunction;
    this.nodeValueComparator = new Comparator(compareFunction);
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {
    if (this.nodeValueComparator.equal(this.value, null)) {
      this.value = value;

      return this;
    }

    if (this.nodeValueComparator.lessThan(value, this.value)) {
      // Insert to the left.
      if (this.left) {
        return this.left.insert(value);
      }

      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      this.setLeft(newNode);

      return newNode;
    }

    if (this.nodeValueComparator.greaterThan(value, this.value)) {
      // Insert to the right.
      if (this.right) {
        return this.right.insert(value);
      }

      const newNode = new BinarySearchTreeNode(value, this.compareFunction);
      this.setRight(newNode);

      return newNode;
    }

    return this;
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  find(value) {
    // Check the root.
    if (this.nodeValueComparator.equal(this.value, value)) {
      return this;
    }

    if (this.nodeValueComparator.lessThan(value, this.value) && this.left) {
      // Check left nodes.
      return this.left.find(value);
    }

    if (this.nodeValueComparator.greaterThan(value, this.value) && this.right) {
      // Check right nodes.
      return this.right.find(value);
    }

    return null;
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {
    return !!this.find(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {
    const nodeToRemove = this.find(value);

    if (!nodeToRemove) {
      throw new Error('Item not found in the tree');
    }

    const { parent } = nodeToRemove;

    if (!nodeToRemove.left && !nodeToRemove.right) {
      // Node is a leaf and thus has no children.
      if (parent) {
        // Node has a parent. Just remove the pointer to this node from the parent.
        parent.removeChild(nodeToRemove);
      } else {
        // Node has no parent. Just erase current node value.
        nodeToRemove.setValue(undefined);
      }
    } else if (nodeToRemove.left && nodeToRemove.right) {
      // Node has two children.
      // Find the next biggest value (minimum value in the right branch)
      // and replace current value node with that next biggest value.
      const nextBiggerNode = nodeToRemove.right.findMin();
      if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) {
        this.remove(nextBiggerNode.value);
        nodeToRemove.setValue(nextBiggerNode.value);
      } else {
        // In case if next right value is the next bigger one and it doesn't have left child
        // then just replace node that is going to be deleted with the right node.
        nodeToRemove.setValue(nodeToRemove.right.value);
        nodeToRemove.setRight(nodeToRemove.right.right);
      }
    } else {
      // Node has only one child.
      // Make this child to be a direct child of current node's parent.
      /** @var BinarySearchTreeNode */
      const childNode = nodeToRemove.left || nodeToRemove.right;

      if (parent) {
        parent.replaceChild(nodeToRemove, childNode);
      } else {
        BinaryTreeNode.copyNode(childNode, nodeToRemove);
      }
    }

    // Clear the parent of removed node.
    nodeToRemove.parent = null;

    return true;
  }

  /**
   * @return {BinarySearchTreeNode}
   */
  findMin() {
    if (!this.left) {
      return this;
    }

    return this.left.findMin();
  }
}

BinarySearchTree

import BinarySearchTreeNode from './BinarySearchTreeNode';

export default class BinarySearchTree {
  /**
   * @param {function} [nodeValueCompareFunction]
   */
  constructor(nodeValueCompareFunction) {
    this.root = new BinarySearchTreeNode(null, nodeValueCompareFunction);

    // Steal node comparator from the root.
    this.nodeComparator = this.root.nodeComparator;
  }

  /**
   * @param {*} value
   * @return {BinarySearchTreeNode}
   */
  insert(value) {
    return this.root.insert(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  contains(value) {
    return this.root.contains(value);
  }

  /**
   * @param {*} value
   * @return {boolean}
   */
  remove(value) {
    return this.root.remove(value);
  }

  /**
   * @return {string}
   */
  toString() {
    return this.root.toString();
  }
}

复杂度

时间复杂度

访问	查找	插入	删除
O(log(n))	O(log(n))	O(log(n))	O(log(n))

空间复杂度

O(n)

参考资料

• 维基百科
• YouTube上的插入BST教程
• BST交互式可视化