选择排序

选择排序（Selection Sort）是一种排序算法，具体来说是一种原地比较排序算法。它的时间复杂度是 O(n^2)，在大型列表上效率低下，并且通常比类似的插入排序表现更差。选择排序以其简单性而闻名，在某些情况下，特别是在辅助内存有限的情况下，它在性能上优于更复杂的算法。

算法可视化

算法可视化

选择排序流程

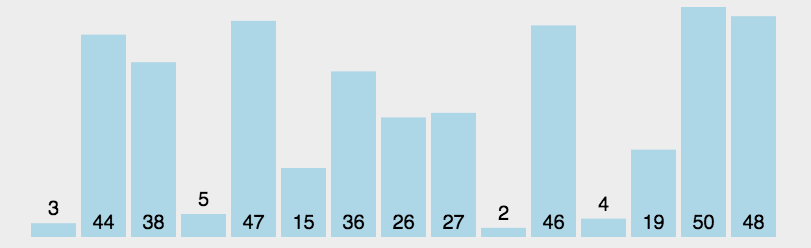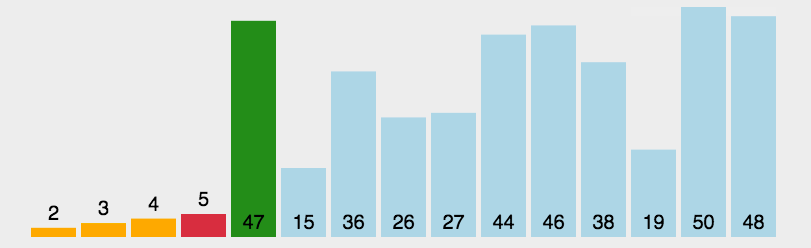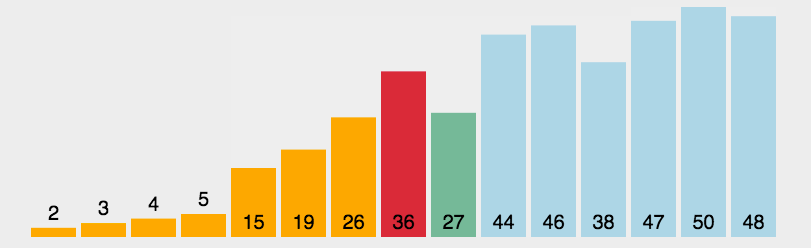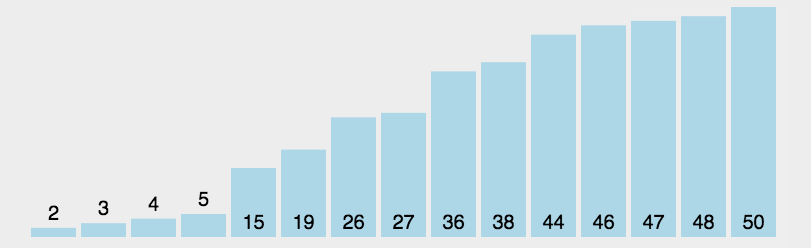
选择排序是一种简单直观的排序算法，它的主要思想是在未排序序列中找到最小（或最大）的元素，然后将其放到已排序序列的末尾。以下是选择排序的步骤：

1. 创建一个函数 selectionSort，它接受一个数组作为参数。
2. 在 selectionSort 函数内部，使用一个循环遍历未排序序列的所有元素，记为 i，并假设当前元素为最小值。
3. 在循环中，再嵌套一个循环用于找到未排序序列中的最小元素的索引，从 i+1 到数组末尾。记最小元素索引为 minIndex。
4. 如果 minIndex 不等于 i，则交换 i 和 minIndex 处的元素，将当前最小元素放到已排序序列的末尾。
5. 循环结束后，数组将按升序排列。

function selectionSort(arr) {
  const len = arr.length;
  
  for (let i = 0; i < len - 1; i++) {
    let minIndex = i;

    for (let j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }

    if (minIndex !== i) {
      [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
    }
  }
  
  return arr;
}

// 示例用法：
const array = [64, 25, 12, 22, 11];
const sortedArray = selectionSort(array);
console.log(sortedArray); // 输出：[11, 12, 22, 25, 64]

selection_sort

选择排序优化

这是基本的选择排序算法实现。接下来，我将介绍一种优化方法，称为“双向选择排序”。

双向选择排序是对传统选择排序的一种改进，它通过同时寻找未排序序列中的最大和最小元素，然后分别将它们放到已排序序列的两端，从而减少了一半的比较次数。

function bidirectionalSelectionSort(arr) {
  let left = 0;
  let right = arr.length - 1;

  while (left < right) {
    let minIndex = left;
    let maxIndex = right;

    for (let i = left; i <= right; i++) {
      if (arr[i] < arr[minIndex]) {
        minIndex = i;
      }

      if (arr[i] > arr[maxIndex]) {
        maxIndex = i;
      }
    }

    if (minIndex !== left) {
      [arr[left], arr[minIndex]] = [arr[minIndex], arr[left]];
    }

    if (maxIndex === left) {
      // 如果最大元素移到了最小元素的位置，更新最大元素的索引
      maxIndex = minIndex;
    }

    if (maxIndex !== right) {
      [arr[right], arr[maxIndex]] = [arr[maxIndex], arr[right]];
    }

    left++;
    right--;
  }

  return arr;
}

// 示例用法：
const array = [64, 25, 12, 22, 11];
const sortedArray = bidirectionalSelectionSort(array);
console.log(sortedArray); // 输出：[11, 12, 22, 25, 64]

双向选择排序的优化使得每一轮循环可以同时找到最大和最小元素，从而减少了比较次数。这样，在大型数据集上，它的性能优于传统的选择排序算法。

复杂度

名称	最佳情况	平均情况	最坏情况	内存	稳定性	备注
选择排序	n^2	n^2	n^2	1	否

参考资料

维基百科