计数排序

在计算机科学中，计数排序（Counting Sort）是一种根据键值为小整数的集合对对象进行排序的算法，也就是说，它是一种整数排序算法。它通过计算具有每个不同键值的对象的数量，并使用这些计数的算术运算来确定每个键值在输出序列中的位置。它的运行时间与项的数量和最大键值与最小键值之间的差异成线性关系，因此仅适用于键的变化不显著大于项的数量的直接使用情况。然而，它经常作为另一个排序算法（基数排序）的子程序使用，后者可以更有效地处理更大的键。

由于计数排序使用键值作为数组的索引，它不是一种比较排序，因此不适用于比较排序的下限 Ω(n log n)。桶排序可以用于与计数排序相同的任务，并且具有类似的时间复杂度分析；然而，与计数排序相比，桶排序需要使用链表、动态数组或大量预分配的内存来保存每个桶中的项目集，而计数排序则将每个桶中存储一个数字（项目的计数）。

计数排序在每个数组元素的数字范围非常小的情况下效果最好。

算法步骤

步骤一

第一步是计算输入数组 A 的所有元素的计数。然后将结果存储在计数数组 C 中。 计数的方法如下图所示。

计数排序

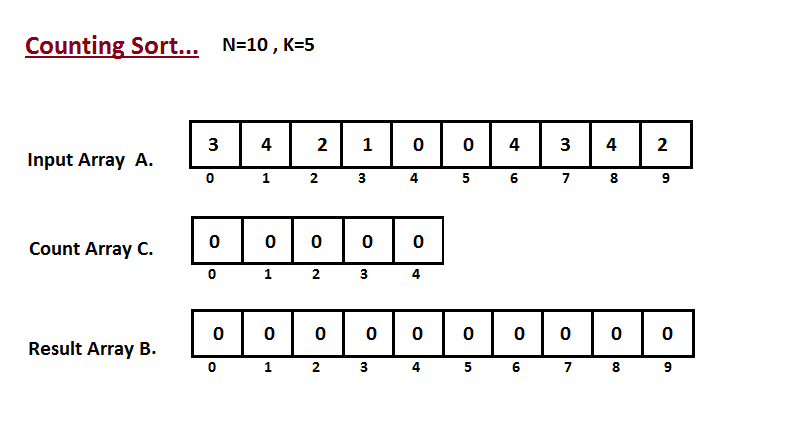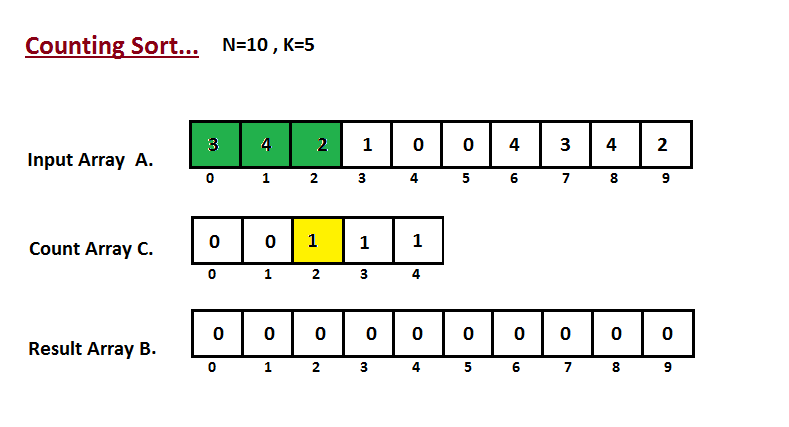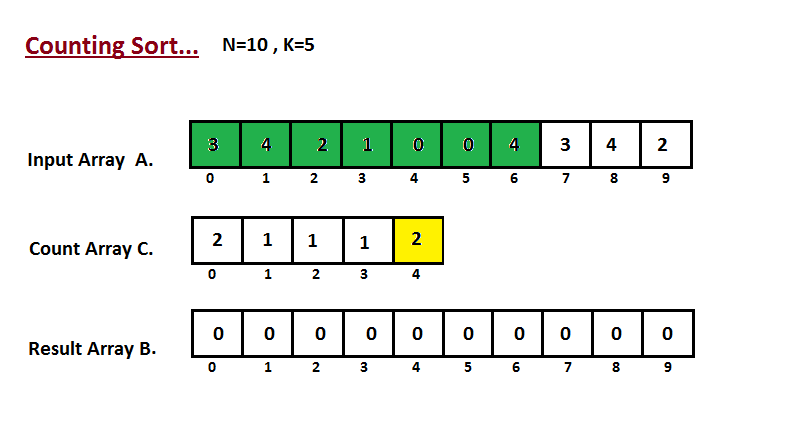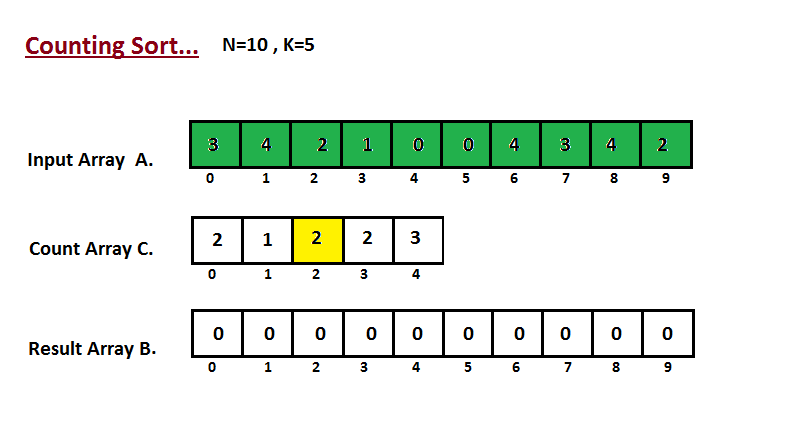
步骤二

第二步是计算在输入数组 A 中存在多少个元素小于或等于给定索引的值。 Ci = 输入数组中小于或等于 i 的元素的数量。

计数排序

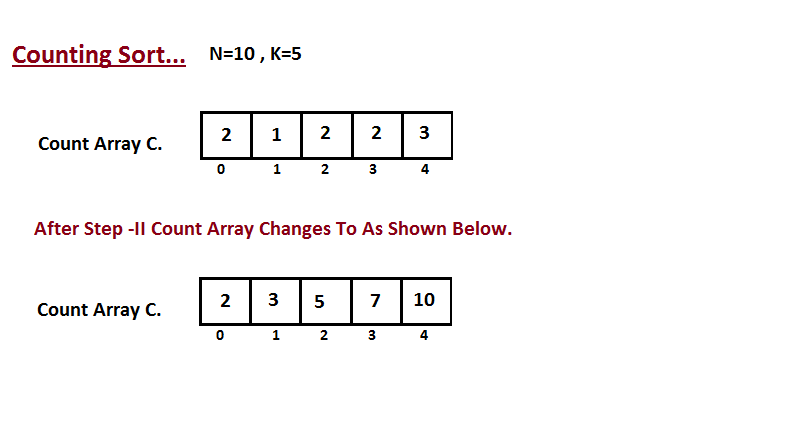
步骤三

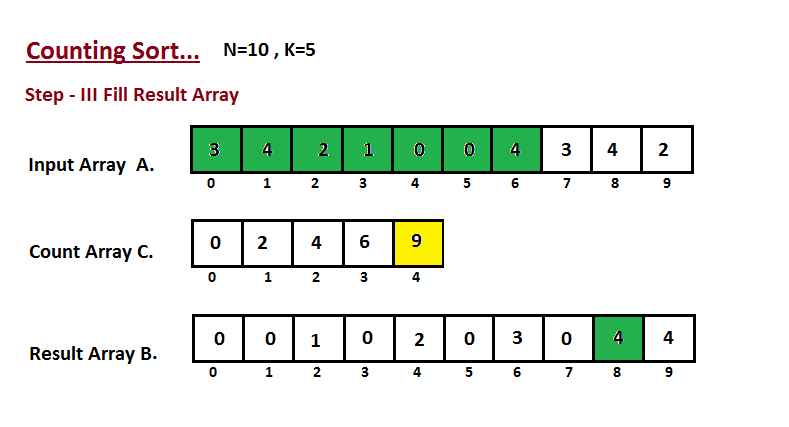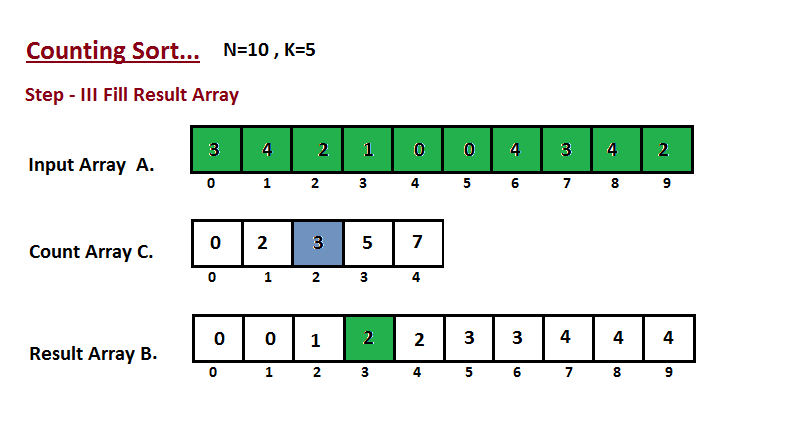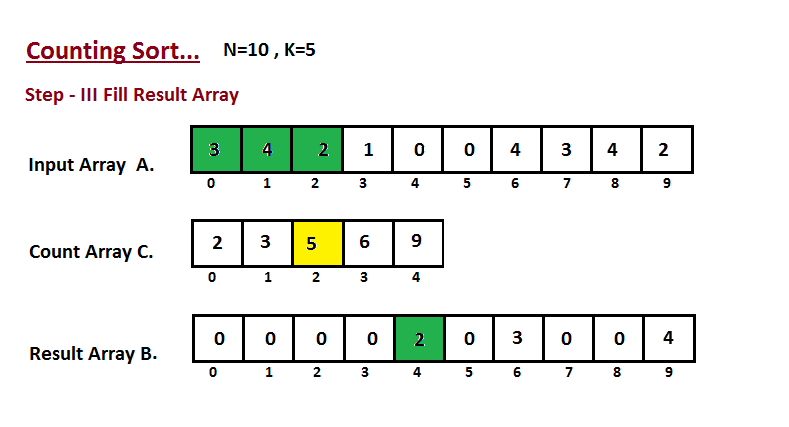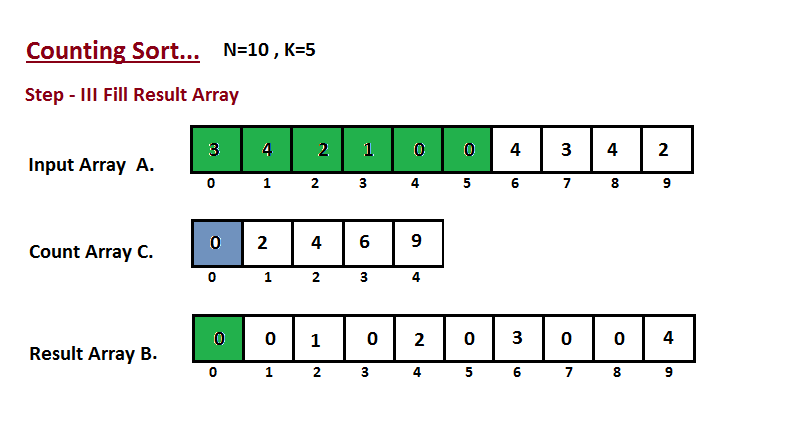
在这一步中，我们根据步骤二中构建的计数数组 C，将输入数组 A 的元素放置在排序位置上。我们使用结果数组 B 来存储排序后的元素。这里我们将 B 的索引从零开始处理。

计数排序

function countingSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }

  // 确定数组的范围
  const max = Math.max(...arr);
  const min = Math.min(...arr);
  const range = max - min + 1;

  // 创建计数数组，并初始化为0
  const countArray = new Array(range).fill(0);

  // 统计每个元素出现的次数
  for (let i = 0; i < arr.length; i++) {
    const countIndex = arr[i] - min;
    countArray[countIndex]++;
  }

  // 根据计数数组重新排序原数组
  let sortedIndex = 0;
  for (let i = 0; i < countArray.length; i++) {
    while (countArray[i] > 0) {
      arr[sortedIndex] = i + min;
      sortedIndex++;
      countArray[i]--;
    }
  }

  return arr;
}

复杂度

名称	最佳情况	平均情况	最坏情况	内存	稳定性	备注
计数排序	n + r	n + r	n + r	n + r	是	r - 数组中的最大数

参考资料

• 维基百科
• YouTube
• EfficientAlgorithms