桶排序
桶排序
桶排序(Bucket Sort)或箱排序(Bin Sort)是一种排序算法,它通过将数组的元素分配到多个桶中来进行排序。然后,每个桶分别进行排序,可以使用不同的排序算法,或者通过递归应用桶排序算法进行排序。
基本原理和排序流程
桶排序是一种线性时间复杂度的排序算法,其基本原理如下:
确定桶的数量:根据待排序元素的范围和分布情况,确定合适的桶的数量。
将元素分配到桶中:遍历待排序的元素,将每个元素根据其值分配到对应的桶中。
对每个桶中的元素进行排序:对每个非空的桶中的元素进行排序。可以使用任何其他排序算法,如插入排序或快速排序。
合并结果:将每个桶中的元素按照顺序依次合并,得到最终的排序结果。
元素被分配到各个桶中:
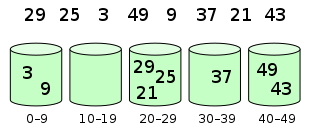
然后,在每个桶内进行排序:

桶排序的优化技巧
尽管桶排序是一种高效的算法,但在某些情况下,其性能可能有所下降。为了克服这些问题,我们可以使用以下优化技巧:
合理选择桶的数量
桶的数量对桶排序的性能有重要影响。过多或过少的桶可能导致不必要的开销或排序结果不准确。为了提高性能,应根据待排序元素的范围和分布情况,合理选择桶的数量。
使用插入排序优化桶内排序
当桶的大小较小时,使用插入排序算法对桶内的元素进行排序通常更高效。插入排序在小规模数据上表现出色,可以减少桶内排序的时间复杂度。
对桶之间的元素进行排序
在某些情况下,桶之间的元素可能已经有序,但由于每个桶内部的排序操作,可能会导致桶之间的元素重新排列。在这种情况下,可以对桶之间的元素进行排序,以进一步优化性能。
完整代码:
function bucketSort(arr, bucketSize = 5) {
if (arr.length === 0) {
return arr;
}
const minValue = Math.min(...arr);
const maxValue = Math.max(...arr);
const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
const buckets = new Array(bucketCount);
for (let i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
for (let i = 0; i < arr.length; i++) {
const bucketIndex = Math.floor((arr[i] - minValue) / bucketSize);
buckets[bucketIndex].push(arr[i]);
}
const sortedArray = [];
for (let i = 0; i < buckets.length; i++) {
if (buckets[i]) {
insertionSort(buckets[i]);
sortedArray.push(...buckets[i]);
}
}
return sortedArray;
}
在这个示例中,我们使用bucketSort函数实现桶排序。我们首先确定桶的数量,根据元素范围和分布计算出合适的桶的数量。然后,我们创建桶数组,并将待排序元素根据值分配到相应的桶中。接下来,对每个非空的桶进行排序,我们可以使用插入排序等算法。最后,将每个桶中的元素按照顺序合并,得到最终的排序结果。
复杂度
桶排序的计算复杂度取决于用于对每个桶进行排序的算法、要使用的桶的数量以及输入是否均匀分布。
当桶内使用的排序算法是插入排序时,桶排序的最坏情况时间复杂度为 O(n^2)。这是最常见的情况,因为预期是每个桶的元素数量相对于整个列表不会太多。在最坏情况下,所有元素都被放入一个桶中,导致运行时间降低到插入排序的最坏情况复杂度(所有元素按逆序排列)。如果所使用的中间排序算法的最坏情况运行时间是 O(n * log(n)),那么桶排序的最坏情况运行时间也将是 O(n * log(n))。
在平均情况下,当元素在桶之间的分布相对均匀时,可以证明桶排序的平均运行时间为 O(n + k),其中 k 是桶的数量。

